Description

This function displays $d_{z}$ for repeated measures data and the non-central confidence interval using the standard deviation of the differences as the denominator.

The formula for $d_{z}$ is: $$d_{z} = \frac{M_1 - M2}{SD{differences}}$$

The formula for t is: $$t = {M_{1} - M_{2}\over SE_{differences}}$$

R Function

d.dep.t.diff(mdiff, sddiff, n, a = .05)

Arguments

  • mdiff = mean difference score
  • sddiff = standard deviation of the difference scores
  • n = sample size
  • a = significance level

Example

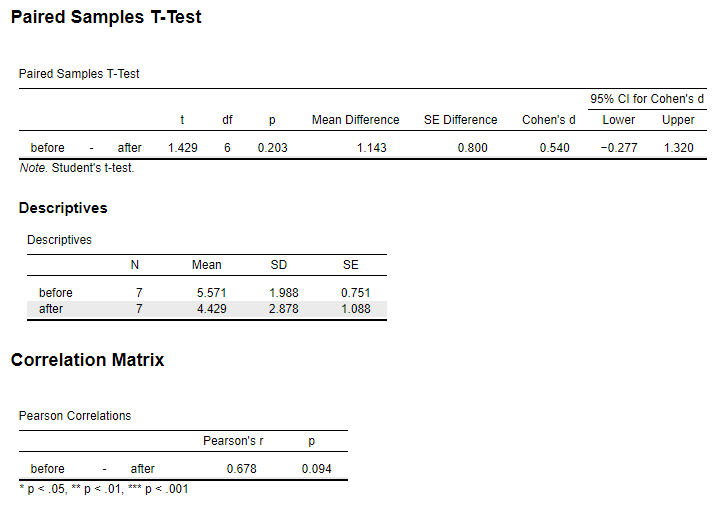
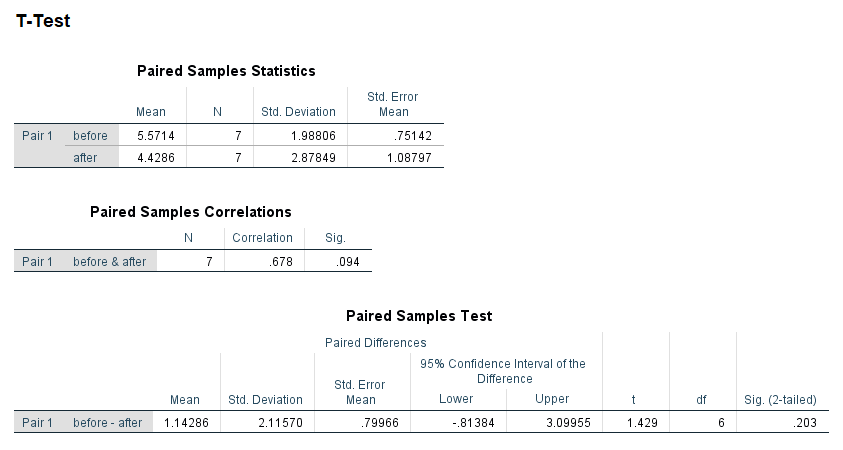
In a study to test the effects of science fiction movies on people’s belief in the supernatural, seven people completed a measure of belief in the supernatural before and after watching a popular science fiction movie. Participants’ scores are shown with high scores indicating high levels of belief. The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP Dependent t JASP

SPSS Dependent t SPSS

SAS Dependent t SAS

Function in R:

d.dep.t.diff(mdiff = 1.143, sddiff = 2.116, n = 7, a = .05)

MOTE

Screenshot

Dependent t Differences - Means Screenshot

Effect Size:

$d_{z}$ = 0.54, 95% CI [-0.03, 1.09]

Interpretation:

Your confidence interval does include zero, and therefore, you might conclude that this effect size is similar to zero.

Summary Statistics:

Mdiff = 1.14, SDdiff = 2.12, SE = 0.57, 95% CI [-0.08, 2.36]

Test Statistic:

t(6) = 1.429, p = .203

Interpretation:

Your p-value is greater than the alpha value, and therefore, this test would be considered not statistically significant.

Tutorial